After a grueling year filled with a wide variety of robot sporting events, we have arrived at the final event of the year: Robot Archery. Four robots have qualified for this year’s finals, and have been seeded in the following order:

Robot   Seed 
Aaron   1
Barron  2
Caren   3
Darrin  4

The robots will take turns shooting arrows at a target [1], starting with Aaron and proceeding in order by seed. When it is a given robot’s turn, they shoot a single arrow. If it is closer to the center of the target than all previous arrows by all players, that robot remains in the tournament, going to the back of the queue to await their next turn. Otherwise that robot is eliminated immediately. The last robot remaining in the queue is the winner.

For example, here is how last year’s finals went, in which Caren was the winner. (Oddly enough it involved the same robots in the same seeding.)

Turn  	Robot	Distance
1       Aaron   10nm
2       Barron  8nm
3       Caren   7nm
4       Darrin  1km
5       Aaron   9nm
6       Barron  2nm
7       Caren   1nm
8       Barron  1Ym [2]

To ten decimal places, what is the probability that Darrin will be this year’s winner? (Or, if you want to send in the exact answer, that’s fine too!)

[1] Each robot is equally skilled. Which is to say: for any region R on the target with nonzero area, the robots all have the same positive probability of landing an arrow within R on any given shot.

[2] It’s a large target.

The first thing we consider is the fact that the actual distance of the arrow is not important. All arrows are independent and identically distributed, so by taking the inverse we can transform the distance into quantiles that follow a \(\text{UNIF}(0, 1)\) distribution.

Furthermore, given that after \(k\) shots we have distances with quantiles \(q_1, \ldots, q_k\), let us calculate the probability of quantile \(Q \sim \text{UNIF}(0, 1)\) being the lower than all other quantiles:

\[\begin{align*} \mathbb{P}(Q < \text{min}\{q_1, \ldots, q_k\}) &= \int_0^1 f_Q(t) \cdot \mathbb{P}(t < \text{min}\{q_1, \ldots, q_k\}) dt \\ &\overset{i.i.d.}{=} \int_0^1 \Pi_{i=1}^k \mathbb{P}(t < q_i) dt \\ &\overset{i.i.d.}{=} \int_0^1 (1-t)^k dt \\ &= \left[- \frac 1 {k+1} \cdot (1-t)^{k+1}\right]^{t=1}_{t=0} \\ &= \frac 1 {k+1} \end{align*}\]

It turns out this probability only depends on the amount of previous arrows. This makes it easy for us to turn this puzzle into a dynamic programming problem. Let \(N \in \mathbb{N}\), then

\[\begin{align*} p &\colon \mathbb{N}^3 \rightarrow \mathbb{R} \\ p&(n, m, k) = \begin{cases} 1, & \text{if } n = 1 \\ \frac 1 {k+1} \cdot p(n, n-1, k+1), & \text{if } m = 0 \\ \frac 1 {k+1} \cdot p(n, m-1, k+1) + \left(1 - \frac 1 {k+1}\right) \cdot p(n-1, m-1, k+1), & \text{otherwise} \end{cases} \end{align*}\]

Where \(N\) stands for the initial amount of players, \(n\) for the amount of players still in the game, \(m\) for the amount of players that still has to shoot before it’s Darrin’s turn, and \(k\) for the amount of arrows that have been shot.

The first case, where \(N=1\), is the case where there is only one player (Darrin) left. In that case the probability of Darrin winning is 1, given that he is the only player left.

In the second case, where \(m=0\), it is currently Darrin’s turn. The only possibility for him to win is if he shoots the closest arrow and then wins the game with this new game state, where there are \(m=n-1\) players that have to shoot the arrow before it is Darrin’s turn again.

The last case is the case where there are still players left, and it is not Darrin’s turn. In that case, you end up with two scenarios you have to take into account. If the current player shoots the closest arrow, he is still in the game (\(n := n\)), but if he does not shoot the closest arrow he gets removed from the game (\(n := n-1\)). Via the law of total probability, we can take the sum these two cases.

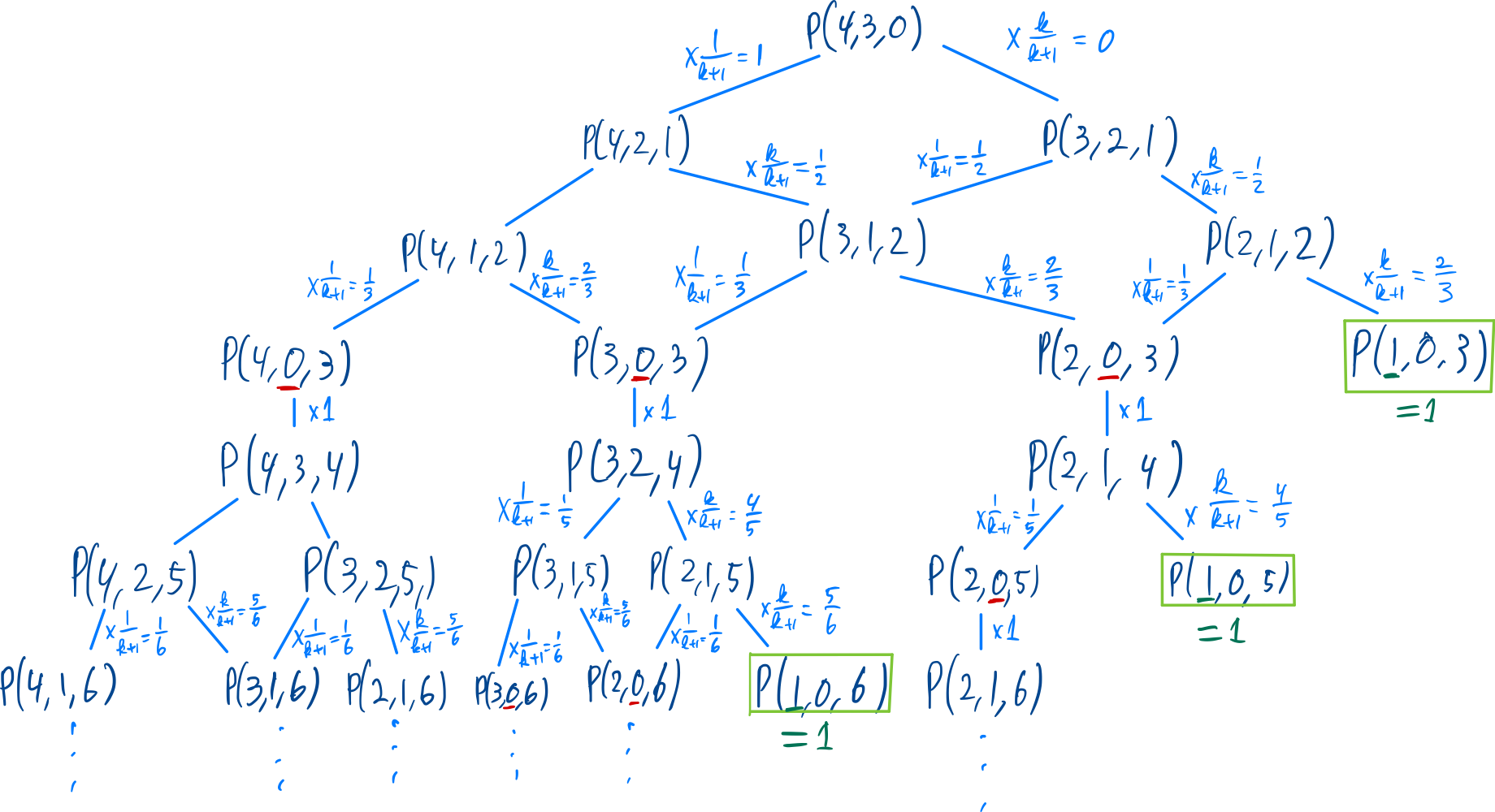
a diagram showing the tree structure of the DP formula above

This way, we have translated our original problem into simply solving \(p(4, 3, 0)\) given \(N=4\). Solving this numerically is not directly possible because we end up in an infinite loop. However, when we consider that we only need ten decimals, and that none of the three cases contribute more to the total sum than \(\left(\frac 1 {k+1}\right)^{k-4}\), we can simply evaluate this problem to a depth of \(k \approx 24\) to get an accurate enough answer: \(p(4,3,0) \approx 0.18343765086\).